Required to Factor a 2048 Bit RSA Integer
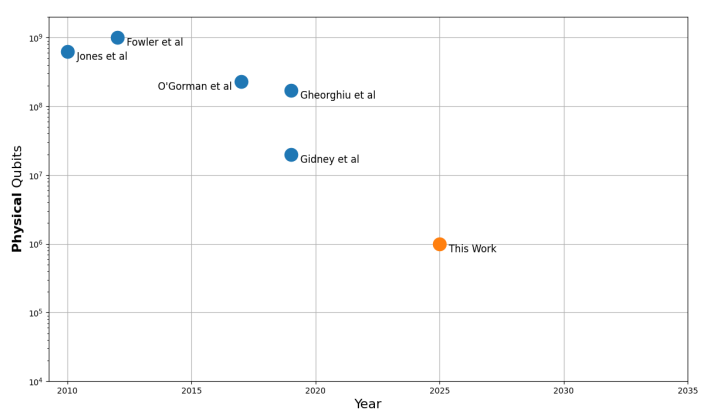
In 2019, co-authors Craig Gidney and Martin Ekerå published a technical paper titled How to factor 2048 bit RSA integers in 8 hours using 20 million noisy qubits. It describes a potential approach based upon Shor’s algorithm and several subsequent research that would be able to factor this type of integer in an 8 hour period using a fault tolerant quantum computer that had a grid based topology with 4-way connectivity, a physical gate error rate of 10−3, a surface code cycle time of 1 microsecond, and a reaction time of 10 microseconds. Although such a large quantum processor is not on anyone current near or medium-term roadmap, it did point the way to show that a real-world implementation of Shor’s algorithm will be possible in the longer term. Since the vast majority of the encryption used in today’s internet is based upon distributing encryption keys using RSA or similar algorithms, this presents a significant security challenge to the world’s IT infrastructure which will need to be fixed using the Post Quantum Cryptography (PQC) algorithms being standardized by NIST or using Quantum Key Distribution (QKD) which others are working on.
Since then, there has been substantial research to find ways that could implement something more efficient. On the algorithm side, a paper by Oded Regev titled An Efficient Quantum Factoring Algorithm described an improved algorithmic approach. In error correction code research, much research is being conducted on quantum LDPC (q-LDPC) and other codes that provide significant efficiency improvements over the surface code. And on the hardware side, there is significant research being performed for better performing qubits such as cat-qubits, dual rail qubits, and many other types.
But now, a new paper has been released by Craig Gidney from the Google Quantum AI team that describes an approach that could theoretically factor a 2048 bit number with less than a million qubits in under a week’s worth of processing time. The assumptions used in this paper are the same as were used in the 2019 paper, i.e. a square grid of qubits with nearest neighbor connections, a uniform gate error rate of 0.1%, a surface code cycle time of 1 microsecond, and a control system reaction time of 10 microseconds. The improvements in this new paper arise from the use of Magic State Cultivation instead of Magic State Distillation to provide a much more efficient way of generating Toffoli gates (also known as CCZ gates). It also uses two additional approaches called approximate residue arithmetic and storing idle logical qubits with yoked surface codes. The trade-off is an increase in runtime from about 8 hours to 1 week, but the benefit is a 20X reduction in the number of physical qubits needed and about a 100X improvement in the number of Toffoli gates by 100x from previous papers.
The technical paper has been posted as a pre-print on arXiv here. and a blog post from Google can be seen here. So, it has not yet been peer reviewed and there could be issues or problems that could come to light as people took a closer look at it. But, if it holds, it could represent a significant disruption in the industry since several companies do show roadmaps with quantum processors that support a million physical qubits by 2030. Those million qubit processors would still be very expensive and probably only affordable to a nation-state. But having something available in 2030 would represent a significant pull-in of a date we call Q-Day when a quantum computer is able to break RSA encryption.
For additional background on other error correction approaches and new quantum hardware developments you can obtain a GQI report titled The Road to Shor Era Quantum Computing which is available here.
May 23, 2025