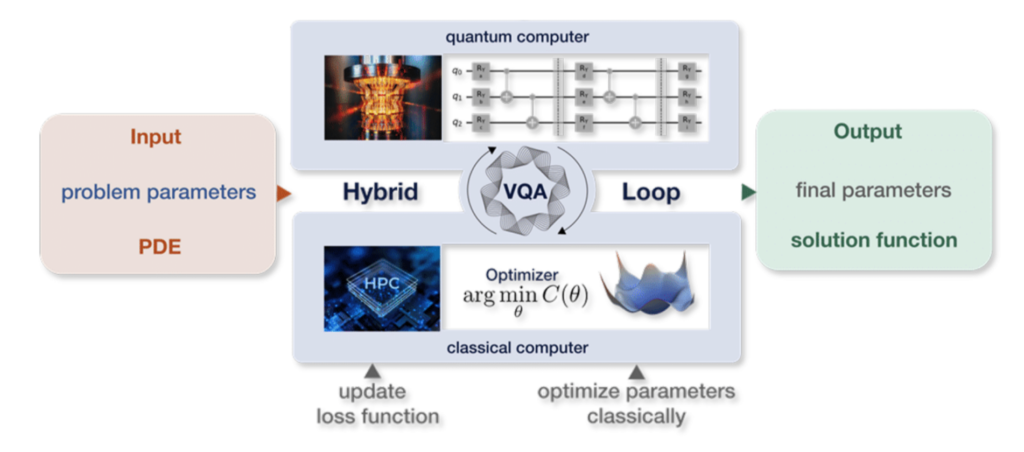
Quantum software company ColibriTD has successfully demonstrated the Hybrid Differential Equation Solver (H-DES) on IBM’s 156-qubit Heron R2 quantum processor, achieving what it describes as the first solution of a partial differential equation (PDE) using a variational quantum algorithm (VQA) on real quantum hardware. The algorithm converged on the inviscid Burgers’ equation using 50 qubits and 10,000 shots per iteration, showcasing the viability of solving nonlinear, high-dimensional PDEs using quantum-enhanced methods.
H-DES addresses the curse of dimensionality in classical solvers by encoding candidate solutions into parameterized quantum circuits, then classically optimizing the residual of the target PDE. Unlike mesh-based classical methods, H-DES uses spectral decomposition into orthogonal polynomial bases, allowing for shallow circuits and generalizable approximations without derivative estimation. In the test case, ColibriTD achieved a final loss below 0.05 after 160 iterations on IBM’s Heron hardware. The company emphasizes that the solution was achieved without extensive error mitigation, demonstrating robustness of the method under noisy intermediate-scale quantum (NISQ) conditions.
In comparison with prior quantum attempts to solve PDEs—many of which failed to converge or were limited by noise—ColibriTD’s H-DES is notable for its algorithmic stability and scalability. The company plans to extend H-DES to support stochastic and integro-differential equations, and aims to transition from the Heron processor to IBM’s forthcoming Flamingo platform, which offers more qubits and reduced error rates. ColibriTD’s goal is to integrate H-DES into its QUICK platform, targeting users of classical engineering tools with an accessible quantum computing interface. These developments could make quantum-powered multiphysics simulations a practical component of industrial workflows in aerospace, fluid dynamics, weather modeling, and beyond.
Read the official blog post here, the whitepaper here, and the arXiv paper here.
March 28, 2025