Researchers from The University of Tokyo and IBM have demonstrated Krylov Quantum Diagonalization (KQD) on an IBM Heron quantum processor, successfully simulating the Heisenberg model on a 2D heavy-hex lattice of up to 56 sites. This experiment represents the simulation of one of the largest many-body systems achieved on a quantum processor to date. The findings of this research have been published in Nature Communications.
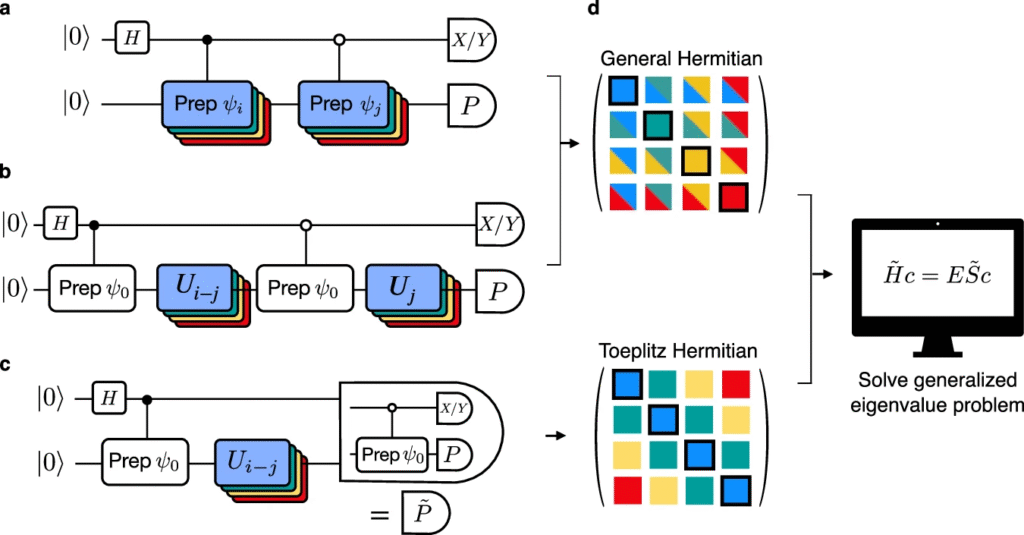
KQD is an algorithm designed for high-precision energy estimation from dynamic behavior, operating without requiring variational optimization. The method constructs subspaces of the many-body Hilbert space using Trotterized unitary evolutions executed on the quantum processor, with subsequent classical diagonalization of many-body interacting Hamiltonians within those subspaces to estimate ground-state energies. The experiments utilized the IBM Heron processor and incorporated advanced error mitigation techniques, including probabilistic error amplification (PEA) and twirled readout error extinction (TREX), alongside Pauli twirling and dynamical decoupling, to address hardware noise and improve the accuracy of measured observables.
This demonstration indicates that quantum systems relevant to condensed matter physics, quantum chemistry, and high-energy physics can be studied on current quantum processors, even prior to the achievement of full fault tolerance. The KQD approach offers exponential convergence towards an estimate of the ground state energy, providing an alternative to traditional variational quantum algorithms. This work marks an advance in the state of the art in quantum simulation, exceeding the scale of prior experimental demonstrations in terms of both qubit count and Hilbert space dimension.
Read the full paper in Nature Communications here.
June 25, 2025