GQI has been working hard to research quantum use cases along with the algorithms that are used and the performance level of the quantum processor required to successfully provide solutions for the use cases. We are making a major effort on this because almost daily we hear the common question of When will we be able to do something commercially useful with a quantum computer? As part of this effort, we have cataloged hundreds of use cases and are adding to this collection on a daily basis.
One of the projects in this effort is that we are writing code and running Quantum Resource Estimates (QRE) for these use cases using assumptions for different quantum processor configurations. The outputs of the QRE runs provide estimates of the machine runtime as well as the number of physical qubits and physical runtime required for each particular algorithm.
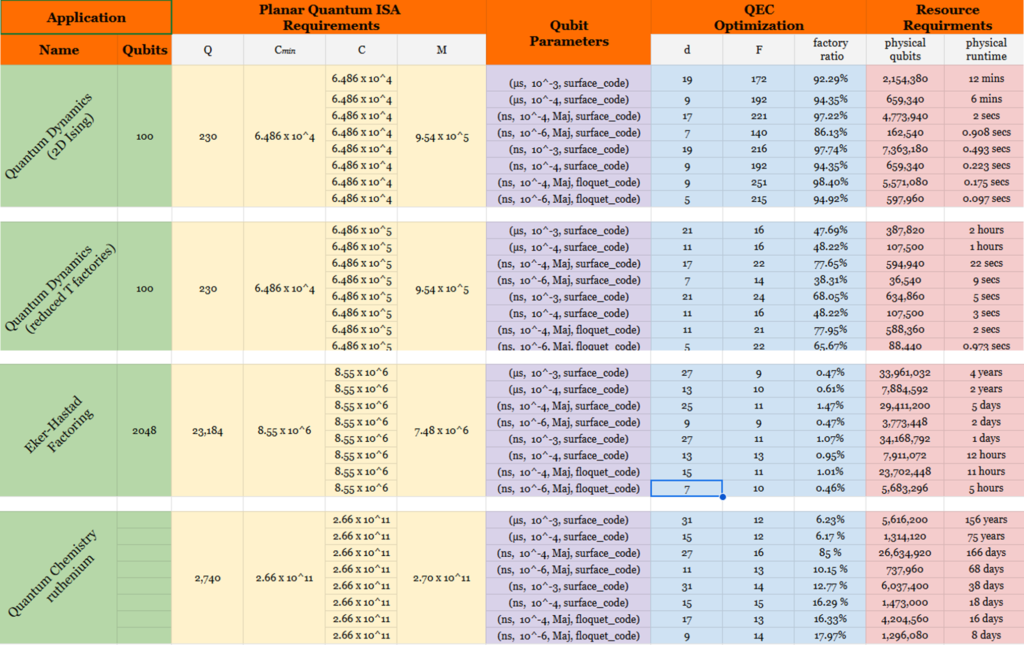
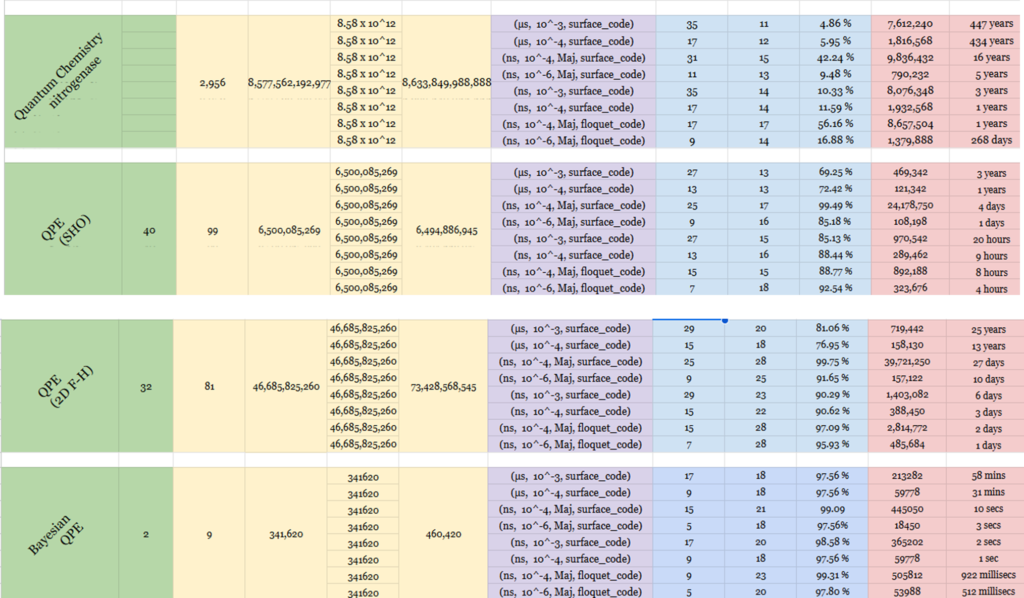
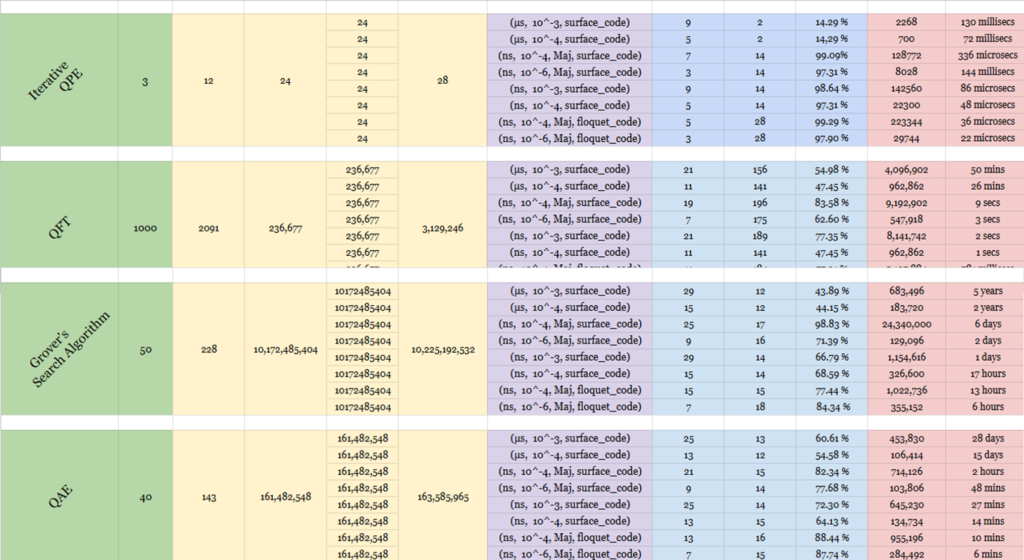
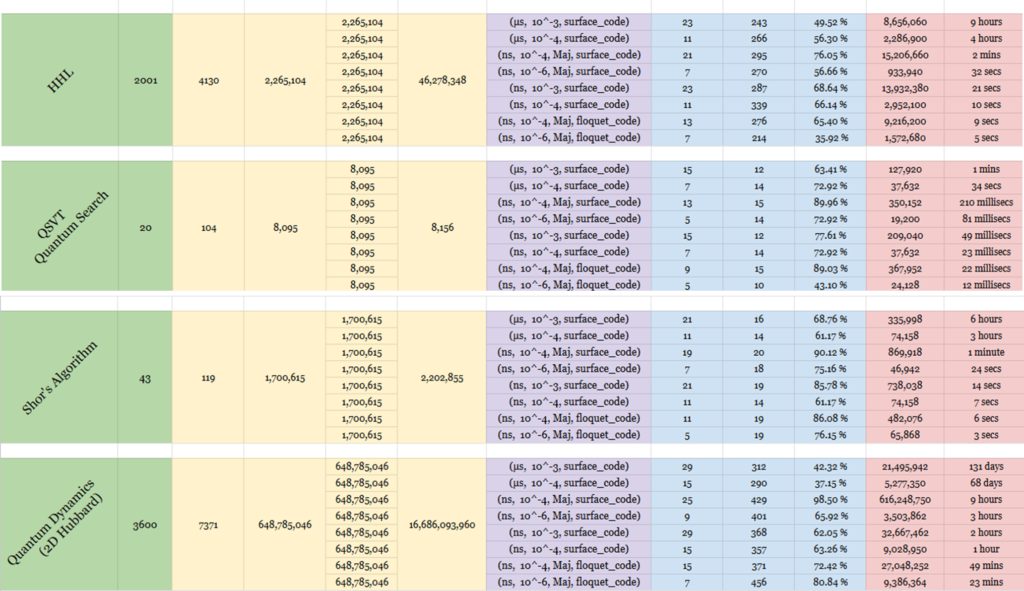
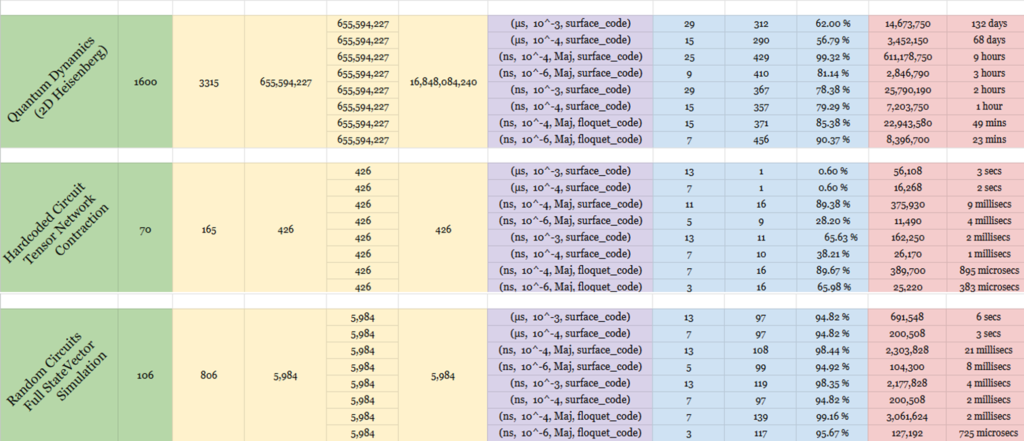
We provided an initial report on this effort last August and are now providing this update to include several more algorithms that we have added since then. As shown in the table below, we have now performed quantum resource estimation for 19 different algorithms on eight different hardware configurations for the use cases as described below:
- Quantum Dynamics is a simulation of Hamiltonian dynamics of important physical systems, using unitary time evolution with a fourth-order Trotter algorithm, such as:
- (2D Ising) a 2D transverse-field Ising model with 100 quantum spins, propagate for ten time-steps.
- (Reduced T factories) is the same use case as above with the number of T factories reduces to show the trade off of qubits needed and runtime.
- (2D Hubbard) 2D Hubbard model of interacting particles on a square lattice of 3600 spins, propagate for 10,000 time-steps.
- (2D Heisenberg) 2D Heisenberg model of interacting spins on a 2D lattice of 1600 spins, propagate for 10,000 time-steps.
- Factoring calculates the pair of prime factors of a 2048 bit integer
- Quantum Chemistry (Ruthenium) calculates the energy of a ruthenium-based catalyst for carbon fixation
- Quantum Chemistry (Nitrogenase) demonstrates the application of quantum computing to explore reaction mechanisms in complex chemical systems, specifically focusing on biological nitrogen fixation in nitrogenase.
- Quantum Phase Estimation (SHO) utilized to analyze the energy spectrum of unitary oracles, focusing on estimating the phase (energy) of a particle confined in a simple harmonic oscillator trap. This method serves as a fundamental tool for dissecting basic systems in physics.
- Quantum Phase Estimation (2D Hubbard) focusing on estimating the phase (energy) of 16 interacting quantum spins on a square lattice. This method serves as a fundamental tool for dissecting complex systems in physics.
- Bayesian QPE is an example of a QPE applications in calculating an inner product between two 2-dimensional vectors and estimating the energy of a simple Hamiltonian while integrating Bayesian statistics in the phase estimation process.
- Iterative QPE is another example of a QPE application which represents the most basic application among the discussed cases, potentially explaining why its estimates are an order of magnitude lower.
- QFT demonstrates capabilities in solving problems in number theory and quantum physics, applying QFT to a uniformly prepared state ∣ + ⟩.
- Grover’s Search Algorithm designed to efficiently identify the unique input that leads to a specific output value in a black box function. It achieves this with a significantly higher probability and speed compared to classical search methods.
- Quantum Amplitude Estimation (QAE) utilizes advance quantum computing’s capacity to resolve complex computational problems by estimating amplitudes of a given quantum state with high precision.
- HHL utilized for solving linear systems of equations, specifically of the form Ax=b where A is a Hermitian matrix and b is a vector. Essentially, it uses inverse QPE to estimate the solution
.
- Quantum Singular Value Transformation (QSVT – Quantum Search) is a cutting-edge framework for gate-based quantum computation that efficiently represents a broad range of polynomial transformations, including non-unitary ones. This framework broadens the scope of possible applications during the NISQ-era and enhances the versatility of quantum algorithms overall.
- Shor’s Algorithm particularly renowned for its potential to factor large integers efficiently, a task that is computationally infeasible for classical computers. Its significance is profound as it poses a threat to current cryptographic methods, including RSA encryption, which relies on the difficulty of factorizing large numbers.
- Hard Coded Circuit for Tensor Network Contraction simulates tensor network contractions, specifically designed to mimic the scenarios described in a study about large-scale classical simulations of quantum circuits by the Alibaba Cloud Quantum Development Platform.
- Random Circuits for Full State Vector Simulation simulates random quantum circuits for full state vector simulation, as explored in the referenced AWS ParallelCluster study. The code aims to dynamically generate and execute quantum circuits of varying complexity.
The Quantum Resource Estimates shown in the table and image below were generated using the Microsoft Azure Quantum Resource Estimator tool which provides resource estimates for programs running on fault tolerant machines (the tool does not support NISQ processors). A previous article posted on the Quantum Computing Report about this tool can be seen here. A complete overview of the Azure Quantum Resource Estimator is available in a technical paper posted on arXiv here. Additional information about this tool is available on Microsoft’s website in blog posts here, here, and here. The open source for this tool is available on GitHub here.
This tool has a large number of parameters that can be used to specify the parameters of the quantum processor being used as well as the ECC code. Details on how to do that are explained in the references listed above. For the results provided table shown below, here are the definitions of the parameters that were used as the inputs and outputs for the tests we ran.
- Q Number of Logical Qubits
- Cmin Minimum Local Time Steps
- C Logical Time Steps
- M Number of T States
- d Code Distance
- f Number of T State Distillation Factories
- Factory Percentage of Physical Qubits Used
Ratio T State Distillation Factories - Physical Number of Physical Qubits to Run the Algorithm with the
Qubits Specified Machine
The characteristics of the target quantum computer can be specified as well. These include things like gate delays, measurement times, QEC code scheme, error budgets, constraints, etc. The Azure Quantum Resource Estimator includes eight pre-defined sets of qubit parameters which we used in the table above. These are noted as follows:
(us, 10-3)SC 100 usec. gate times, 10-3 error rate, surface code.
Possible ion trap processor
(us, 10-4)SC 100 usec. gate times, 10-4 error rate, surface code.
Possible ion trap processor
(ns, 10-3)SC 100 nsec. gate times, 10-3 error rate, surface code.
Possible superconducting processor
(ns, 10-4)SC 100 nsec. gate times, 10-4 error rate, surface code.
Possible superconducting processor
(ns, 10-4)SC 100 nsec. gate times, 10-4 error rate, surface code.
Possible Majorana processor
(ns, 10-6)SC 100 nsec. gate times, 10-6 error rate, surface code.
Possible Majorana processor
(ns, 10-4)FC 100 nsec. gate times, 10-4 error rate, floquet code.
Possible Majorana processor
(ns, 10-6)FC 100 nsec. gate times, 10-6 error rate, floquet code.
Possible Majorana processor
Results
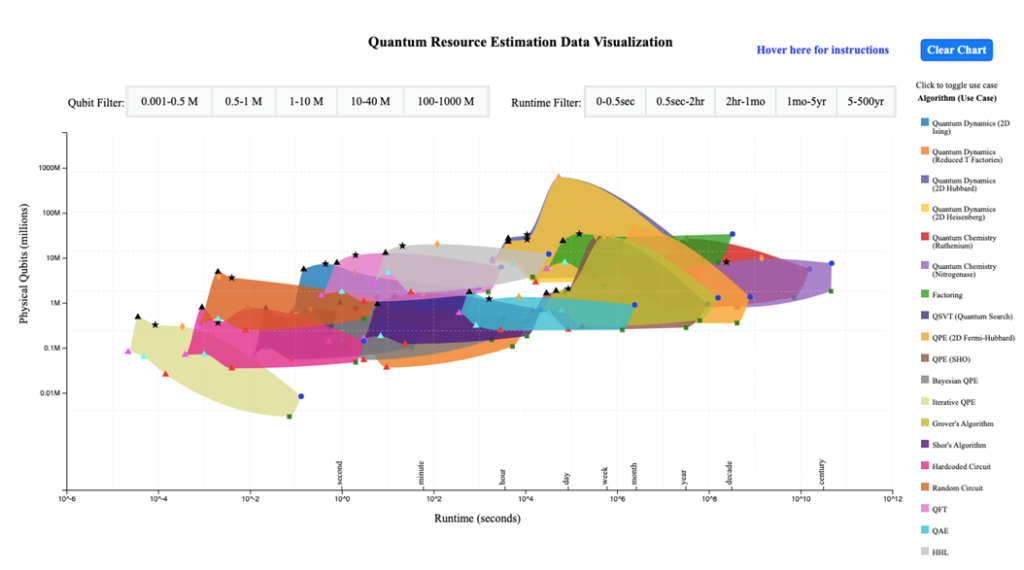
The results vary greatly depending upon the particular algorithms and the machine configurations that it simulates. In the analysis shown, the number of physical qubits can vary anywhere from 700 qubits to 34 million. And the physical runtimes of the algorithms can vary anywhere from 22 microseconds to 447 years. We show this in the chart below which is displayed on a log-log scale. Click on the chart to see our Quantum Resource Estimation Visualization Tool provides the data in a dynamic and clearer way.
For additional information about this topic, you can view our previous article on this topic here. And if you are interested in learning more about our research study expanding our data base of quantum use cases and quantum resource estimates, contact us at info@global-qi.com for more information.
January 20, 2025