(Controlled Hadamard on Left, T-Gate using Code Switching on Right)
We have reported in the QCR recently on several research projects to create quantum error correction codes (see here, here, here, and here), but one of the most significant challenges for implementing a full fault tolerant quantum computer is being able to robustly support a complete, universal gate set that could conceivably implement any quantum algorithm. It is one thing to create logical qubits using a specific error correction code, but it is another thing to be able to perform gate operations on those qubits to do something useful.
When one examines the types of gates that need to be implemented, they can be divided into two categories, Clifford gates and Non-Clifford gates. A set of Clifford gates would include the Hadamard, CNOT, and S (Phase gate). From these many of the other common gates can be synthesized. However, the Clifford set is not sufficient or running any quantum algorithm nor is it able to provide a quantum advantage over a classical algorithm, per the Gottesman-Knill theorem. In order to achieve full advantage, one needs to implement non-Clifford gates such as the T-gate, the Toffoli gate or other non-Clifford gates. When both the gates from the Clifford group as well as a non-Clifford gate are available, the quantum computer will have a universal gate set that can conceivably process any quantum algorithm and provide a speedup over a classical implementation.
A popular technique for implementing the non-Clifford gates is called Magic State Distillation. But this approach requires a lot of resources to implement and can require using the majority of the qubits available in the processor. Quantinuum has researched two different approaches for creating non-Clifford gates for quantum error correction, demonstrated them on their ion trap quantum processors with record logical gate fidelities, and posted technical papers describing this research.
The first paper created magic states with infidelities of about 7 x 10-5 to implement a non-Clifford gate called the Controlled-Hadamard (CH) on their H1-1 processor with a logical infidelity of less than 2.3 x 10-4. This is an order of magnitude better than the unencoded physical CH infidelity of 10−3. The approach uses a [[6,2,2]] code to prepare two |H+⟩ magic states. The process uses two additional ancilla qubits to measure the result and retry the generation if the check is not successful. Experimental results from the paper indicated that this occurred about 14.8% of the time. In the future, they will be able to be concatenated the code to produce a [[36,4,4,]] code block that would produce 4 magic states with infidelities in the 10-10 to 10-14 range. However, they haven’t been able to show this yet since the H1-1 machine only contains 20 qubits. But we would expect them to demonstrate this once their larger machines become available.
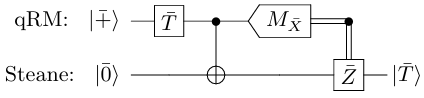
The second paper, which Quantinuum wrote with researchers from the University of California at Davis and the Sandia National Laboratory uses a technique called “code switching”. This code first generates a logical T magic state using a [[15,1,3]] quantum Reed-Muller code. However, that code does not support the other gate types. In this demonstration, the team used the [[7,1,3]] Steane code to implement the other gate types. The logical T state generated by the quantum Reed-Muller is then transferred to the Steane code block using logical one-bit teleportation by a circuit as shown below which will provide them with the full universal gate set.
This demonstration was performed on Quantinuum’s H2-1 proccessor and used 22 data qubits with 6 ancilla qubits for checking. This approach also measured the result with ancilla qubits and redid the T state generation if the initial result wasn’t good. The acceptance rate reported in the paper was about 82%.
Quantinuum has gone further than anyone else in actually creating magic states and a universal gate set on a real quantum processor that have good performance. However, this series of tests have been limited by the size of their current generation of processors. The next step will be to scale up this work to build a larger universal fully fault-tolerant quantum computer with repeatable error correction that can leverage the quantum error correction to do something useful.
For more about this research, you can access a blog post describing it on the Quantinuum website here as well as the two technical papers posted on arXiv here and here.
June 27, 2025